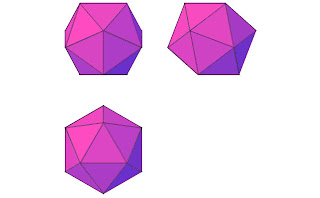
Superficie poliédrica es la que está constituida por varios planos que se cortan entre sí.
Poliedros regulares son los que tienen todas las caras iguales, y son polígonos regulares,-figuras planas que tienen todos los lados y ángulos iguales. Existen sólo cinco y tienen numerosas propiedades: se pueden inscribir unos dentro de otros de diversas formas, se pueden inscribir y circunscribir en una esfera, se pueden prolongar sus aristas obteniéndose otro de ellos, etc. En la figura se observa un icosaedro regular, que es una figura de 20 caras que son polígonos regulares, con sus dos proyecciones planas idénticas en planta y alzado tras un giro de 90° y desplazamiento de una de las vistas.
Pincha en el enlace para bajar un manual sobre los poliedros regulares:
http://www.box.net/shared/lpxg66qqvg
Ejemplos de transformación de superficies poliédricas:
http://inscripcionpoliedrica.blogspot.com/
http://dodecaedro-regular.blogspot.com/
http://icosaedro-regular.blogspot.com/
http://transformacion-de-poliedros.blogspot.com/
http://icosaedroendodecaedro.blogspot.com/
http://superficiespoliedricas.blogspot.com/
http://transformaciondesuperficies.blogspot.com/
http://lospoliedrosregulares.blogspot.com/
http://superficiestransformadas.blogspot.com/
http://metamorfosisgeometrica.blogspot.com/

poliedro de 12 caras pentagonales regulares, en el número 3 observamos esa figura
en axonometría isométrica, en el número 40 vemos la misma figura que contiene a
un cubo inscrito y que pasa por algunos de sus vértices, en la figura número 5 podemos
observar que los tres ejes ortogonales- en color rojo- tienen el mismo tamaño,
eso quiere decir que podemos inscribir también en el dodecaedro regular un octaedro regular
- en color amarillo- tal y como aparece en la figura 6.
dodecaedro regular, observamos además en la figura las proyecciones en
planta y alzado del octaedro regular inscrito en la figura.
Sección oblicua de cono en diédrico y desarrollo
Desarrollo de esfera y ejemplo práctico
 Desarrollar una superficie es extenderla sobre un plano, es coger sus caras y anexionarlas en un plano poniéndolas unidas por sus lados hasta convertirla en una figura plana, de manera que si se recortan los bordes y se doblan por los lados se puede construir en tres dimensiones.
Desarrollar una superficie es extenderla sobre un plano, es coger sus caras y anexionarlas en un plano poniéndolas unidas por sus lados hasta convertirla en una figura plana, de manera que si se recortan los bordes y se doblan por los lados se puede construir en tres dimensiones. Aquí observamos el desarrollo de otra superficie, el cuboctaedro rombitruncado. Esta superficie es un poliedro arquimediano, obtenido por la sección de las caras de un poliedro regular.
Aquí observamos el desarrollo de otra superficie, el cuboctaedro rombitruncado. Esta superficie es un poliedro arquimediano, obtenido por la sección de las caras de un poliedro regular. Diagrama de Schlegel. Si observamos una figura de cristal muy cerca de manera que todas sus aristas queden detrás de una cara, estaremos viendo la figura representada en este diagrama. Para construir figuras según este procedimiento se tiene que dar el caso de que las aristas no se corten entre sí y al mismo tiempo aparezcan todos los vértices y aristas de la figura en su representación. Este diagrama facilita que en las superficies poliédricas, el control de los vértices, de las líneas que pasan por cada vértice, de los lados, etcétera.
Diagrama de Schlegel. Si observamos una figura de cristal muy cerca de manera que todas sus aristas queden detrás de una cara, estaremos viendo la figura representada en este diagrama. Para construir figuras según este procedimiento se tiene que dar el caso de que las aristas no se corten entre sí y al mismo tiempo aparezcan todos los vértices y aristas de la figura en su representación. Este diagrama facilita que en las superficies poliédricas, el control de los vértices, de las líneas que pasan por cada vértice, de los lados, etcétera. Prisma de base hexagonal regular recto. Un prisma es una superficie poliédrica reglada desarrollable. Si las aristas laterales que unen las bases son oblicuas respecto a ellas estaremos hablando de un prisma oblicuo, si no lo son, hablaremos de un prisma recto.
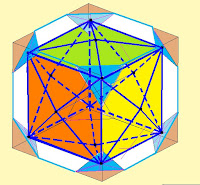
Prisma de base hexagonal regular recto. Un prisma es una superficie poliédrica reglada desarrollable. Si las aristas laterales que unen las bases son oblicuas respecto a ellas estaremos hablando de un prisma oblicuo, si no lo son, hablaremos de un prisma recto. Poliedros duales como el icosaedro y el dodecaedro tienen una propiedad curiosa: si prolongamos las aristas del icosaedro regular se cortan en vértices que determinan los puntos de un dodecaedro. Recíprocamente si prolongamos las aristas del dodecaedro regular se cortan en vértices que determinar los puntos de un icosaedro. Ambas figuras, junto con el cubo en el que se pueden inscribir, tienen sus aristas relacionadas en una proporción áurea. La arista del dodecaedro más la arista del icosaedro es igual a la arista del cubo en el que están inscritos. La relación anterior además de la siguiente pone en relación a los tres elementos en la proporción áurea: la arista del cubo es a la arista del icosaedro como la del icosaedro es a la del dodecaedro, en geometría se dice que la arista del icosaedro es media proporcional entre la arista del cubo y la arista del dodecaedro.
Poliedros duales como el icosaedro y el dodecaedro tienen una propiedad curiosa: si prolongamos las aristas del icosaedro regular se cortan en vértices que determinan los puntos de un dodecaedro. Recíprocamente si prolongamos las aristas del dodecaedro regular se cortan en vértices que determinar los puntos de un icosaedro. Ambas figuras, junto con el cubo en el que se pueden inscribir, tienen sus aristas relacionadas en una proporción áurea. La arista del dodecaedro más la arista del icosaedro es igual a la arista del cubo en el que están inscritos. La relación anterior además de la siguiente pone en relación a los tres elementos en la proporción áurea: la arista del cubo es a la arista del icosaedro como la del icosaedro es a la del dodecaedro, en geometría se dice que la arista del icosaedro es media proporcional entre la arista del cubo y la arista del dodecaedro. Aquí observamos una proyección axonométrica del icosaedro al que se han prolongado sus aristas y en su intersección se generan los vértices de un dodecaedro regular. Al añadir las pirámides hemos obtenido el gran dodecaedro estrellado.
Aquí observamos una proyección axonométrica del icosaedro al que se han prolongado sus aristas y en su intersección se generan los vértices de un dodecaedro regular. Al añadir las pirámides hemos obtenido el gran dodecaedro estrellado.Se puede obtener por tanto un poliedro estrellado al incorporar pirámides en cada una de las caras de un poliedro regular, de esta forma sobre el icosaedro con las pirámides sobre sus caras también los vértices se inscriben en un dodecaedro regular.
 Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.
Las esferas geodésicas son superficies poliédricas adecuadas a esferas. Se pueden construir partiendo de un poliedro regular en el que se triangulan sus caras. Cada nueva triangulación del nuevo vértice que obtenemos, debe estar inscrito en la esfera, generando la superficie más homogénea posible, aunque esto a veces no sea posible teniendo que producir superficies cuyos triángulos no siempre son todos equiláteros.Esfera geodésica hexaédrica de frecuencia 2
http://youtu.be/L9txE6QS_oM
Esfera geodésica octaédrica de frecuencia 2
http://youtu.be/j1-IH6nDJ9E
Esfera geodésica octaédrica de frecuencia 3
http://youtu.be/AtBK88YRGmY
Esfera geodésica octaédrica de frecuencia 3 con proyecciones diédricas iguales
http://youtu.be/6RC4JfP9Eqc
Esfera geodésica octaédrica de frecuencia 4.
http://youtu.be/D1ZZkYXNBys
Esfera geodésica dodecaédrica de frecuencia 1
http://youtu.be/PbGG8EF6IMc
Esfera geodésica dodecaédrica de frecuencia 2
http://youtu.be/hG35S3RSL3M
Esfera geodésica icosaédrica de frecuencia 2
http://youtu.be/8AtDgFxdHwk
Esfera geodésica icosaédrica de frecuencia 3
http://youtu.be/qQNwmCCm488
Esfera geodésica icosaédrica de frecuencia 4
http://youtu.be/EWmKh2wpIdc
 Los poliedros arquimedianos son superficies regladas desarrollables producidas en la mayor parte de los casos por secciones de los poliedros regulares (en el dibujo, todos se pueden obtener por secciones de los poliedros regulares menos los duplicados en sentidos distintos: el cubo romo y dodecaedro romo). Tienen bastante regularidad y todas las caras de los poliedros arquimedianos son polígonos regulares.
Los poliedros arquimedianos son superficies regladas desarrollables producidas en la mayor parte de los casos por secciones de los poliedros regulares (en el dibujo, todos se pueden obtener por secciones de los poliedros regulares menos los duplicados en sentidos distintos: el cubo romo y dodecaedro romo). Tienen bastante regularidad y todas las caras de los poliedros arquimedianos son polígonos regulares. Cortando los poliedros regulares de manera que el plano corte cada arista en tres partes (corte tipo 2, como en el dibujo) o en 2 partes (tipo 1), obtenemos los poliedros arquimedianos -quedan excluidos los romos o chatos, que en el dibujo anejo aparecen los 4 con caras pentagonales o cuadradas rodeadas de triángulos a lo largo de todas sus aristas, cada uno con su imagen especular:
Cortando los poliedros regulares de manera que el plano corte cada arista en tres partes (corte tipo 2, como en el dibujo) o en 2 partes (tipo 1), obtenemos los poliedros arquimedianos -quedan excluidos los romos o chatos, que en el dibujo anejo aparecen los 4 con caras pentagonales o cuadradas rodeadas de triángulos a lo largo de todas sus aristas, cada uno con su imagen especular:  En la figura de la izquierda observamos un icosidodecaedro - con la línea de tierra de color rojo-, esa figura se obtiene del icosaedro -Con la línea de tierra en color azul- o del dodecaedro cortándolo por un corte de tipo 1, o sea, cogiendo los puntos medios de cada arista y uniendolos, de esta forma obtenemos nuevas aristas y nos sale esta figura que aparece en el centro en color verde, en la parte superior.
En la figura de la izquierda observamos un icosidodecaedro - con la línea de tierra de color rojo-, esa figura se obtiene del icosaedro -Con la línea de tierra en color azul- o del dodecaedro cortándolo por un corte de tipo 1, o sea, cogiendo los puntos medios de cada arista y uniendolos, de esta forma obtenemos nuevas aristas y nos sale esta figura que aparece en el centro en color verde, en la parte superior.-----------------------------
con la figura inscrita dentro del dodecaedro- figuras M y N.
En la siguiente página podemos observar la construcción del rombicosidodecaedro (p. arquimediano) a partir del truncamiento de un icosaedro:
http://transformaciondesuperficies.blogspot.com/
Página en la que se puede ver la construcción de varios poliedros arquimedianos a partir de otros más sencillos, como los regulares.
Transformación de un poliedro regular (icosaedro) en distintos poliedros arquimedianos y regreso a otro poliedro regular: el dodecaedro.
http://arquimedianosendiedrico.blogspot.com/
http://poliedrosregularesyarquimedianos.blogspot.com/
Poliedros duales son aquellos que a veces intercambian caras y vértices, por ejemplo el cubo tiene 8 vértices y 6 caras, igual el octaedro tiene 8 caras y 6 vértices.
A veces también se pueden construir al tomar los puntos medios de cada cara, por ejemplo en el caso del cubo si tomamos los puntos medios de cada cara obtenemos el octaedro que quedará entrado con el cubo de manera que sus vértices están sobre las caras del cubo, recíprocamente podemos coger el octaedro y los centros de sus caras triangulares son los vértices de un cubo inscrito.
Los poliedros de Catalan por ejemplo tienen una esfera inscrita ya que los centros de las caras equidistan del centro del poliedro pero sus vértices no equidistan del centro y por lo tanto no tienen esfera circunscrita. Si hacemos coincidir la esfera circunscrita al arquimediano con la inscrita del poliedro de Catalan podemos observar que el arquimediano queda inscrito dentro del dual de Catalan sin embargo la situación inversa no se da pues no hay una esfera circunscrita al de Catalan ni inscrita al arquimediano por lo tanto no es posible en este caso inscribir el poliedro de Catalan dentro del dual arquimediano.
A continuación mostramos un listado de poliedros arquimedianos y sus duales correspondientes, los de Catalan , más abajo a la izquierda observamos el listado de los poliedros regulares y su dual correspondiente, mientras que en la parte inferior derecha observamos que las de pirámides son los poliedros duales de los prismas mientras que los deltoedros son de los antiprismas.
 Aquí tenemos el ejemplo de un poliedro arquimediano generado por el truncamiento del icosaedro regular.
Aquí tenemos el ejemplo de un poliedro arquimediano generado por el truncamiento del icosaedro regular.Es la figura que se utiliza en los balones de fútbol clásicos, se pensaba hasta no hace mucho que sin gran número de aristas tenía una gran esfericidad (86,74% de redondez), hoy en día se utilizan otros con una estructura más esférica como el rombicosidodecaedro con un 94%.
 Los poliedros de Catalan son superficies duales de los arquimedianos. Los centros de las caras de los de Catalan son vértices de poliedros arquimedianos.
Los poliedros de Catalan son superficies duales de los arquimedianos. Los centros de las caras de los de Catalan son vértices de poliedros arquimedianos. El poliedro anterior en sistema axonométrico.
El poliedro anterior en sistema axonométrico. Los poliedros estrellados se pueden construir de forma general sumando pirámides a las caras de poliedros. Los más estudiados son el pequeño dodecaedro estrellado, el gran dodecaedro, el gran dodecaedro estrellado, y el gran icosaedro. Se pueden transformar unos en otros: el gran dodecaedro en pequeño dodecaedro estrellado y recíprocamente y el gran dodecaedro estrellado en el gran icosaedro y recíprocamente. Fueron estudiados por Kepler, Poinsont, Cauchy, etc.
Los poliedros estrellados se pueden construir de forma general sumando pirámides a las caras de poliedros. Los más estudiados son el pequeño dodecaedro estrellado, el gran dodecaedro, el gran dodecaedro estrellado, y el gran icosaedro. Se pueden transformar unos en otros: el gran dodecaedro en pequeño dodecaedro estrellado y recíprocamente y el gran dodecaedro estrellado en el gran icosaedro y recíprocamente. Fueron estudiados por Kepler, Poinsont, Cauchy, etc. En la figura observamos en sistema diédrico y en vista axonométrica un icosaedro regular al que se le han añadido pirámides sobre sus caras, obteniendo de esta forma un poliedro estrellado.
En la figura observamos en sistema diédrico y en vista axonométrica un icosaedro regular al que se le han añadido pirámides sobre sus caras, obteniendo de esta forma un poliedro estrellado. Poliedros compuestos son los que están formados por varios poliedros que tienen el mismo centro. En la imagen vemos dos icosaedros regulares obtenidos por un giro de uno respecto al otro sobre uno de los ejes que pasa por los vértices.
Poliedros compuestos son los que están formados por varios poliedros que tienen el mismo centro. En la imagen vemos dos icosaedros regulares obtenidos por un giro de uno respecto al otro sobre uno de los ejes que pasa por los vértices.http://poliedroscompuestos.blogspot.com/
 Poliedros de Johnson son aquellos que siendo convexos y sin ser regulares ni arquimedianos, están formados por caras que son polígonos regulares.
Poliedros de Johnson son aquellos que siendo convexos y sin ser regulares ni arquimedianos, están formados por caras que son polígonos regulares. Johnson construyó todos los polígonos que entraban dentro de esta clasificación. En la imagen aparecen unos cuantos.
Johnson construyó todos los polígonos que entraban dentro de esta clasificación. En la imagen aparecen unos cuantos. El dodecaedro truncado y Triaquisicosaedro son dos poliedros duales, el arquimediano se puede inscribir en el de Catalan de forma que en este último tomamos los puntos medios de las caras y los unimos.
El dodecaedro truncado y Triaquisicosaedro son dos poliedros duales, el arquimediano se puede inscribir en el de Catalan de forma que en este último tomamos los puntos medios de las caras y los unimos.http://icosaedrotriakis.blogspot.com/
 Observamos que la recíproca no es cierta y el triaquisicosaedro no se puede inscribir en el dodecaedro truncado de forma que los vértices del poliedro de Catalan estén sobre los puntos medios de las caras del arquimediano.
Observamos que la recíproca no es cierta y el triaquisicosaedro no se puede inscribir en el dodecaedro truncado de forma que los vértices del poliedro de Catalan estén sobre los puntos medios de las caras del arquimediano. Aquí vemos otra vista en la que el arquimediano está inscrito en el de Catalan. El triaquisicosaedro no es otra cosa que el icosaedro con pirámides sobre sus caras, de ahí su nombre con el prefijo triakis-, denominación que designa en los poliedros de Catalan este detalle.
Aquí vemos otra vista en la que el arquimediano está inscrito en el de Catalan. El triaquisicosaedro no es otra cosa que el icosaedro con pirámides sobre sus caras, de ahí su nombre con el prefijo triakis-, denominación que designa en los poliedros de Catalan este detalle.Los poliedros de Catalan poseen una esfera inscrita y los arquimedianos circunscrita
 Si cogemos los puntos medios de las caras de un antiprisma y los unimos con sus vértices más cercanos, obtenemos la figura dual de un antiprisma que es el deltoedro. Es una figura utilizada en dados, ya que puede tener número de caras ilimitada y al ser homogénea y todas sus caras estar en igual disposición respecto al centro, hay las mismas posibilidades de que caiga cualquier cara en un lanzamiento del dado.
Si cogemos los puntos medios de las caras de un antiprisma y los unimos con sus vértices más cercanos, obtenemos la figura dual de un antiprisma que es el deltoedro. Es una figura utilizada en dados, ya que puede tener número de caras ilimitada y al ser homogénea y todas sus caras estar en igual disposición respecto al centro, hay las mismas posibilidades de que caiga cualquier cara en un lanzamiento del dado. Proyección axonométrica de un deltoedro, está formado por caras en forma de Delta, trapezoides con un eje de simetría.
Proyección axonométrica de un deltoedro, está formado por caras en forma de Delta, trapezoides con un eje de simetría. Aquí observamos una dipirámide, es un poliedro formado por dos pirámides unidas, dual del prisma obtenido en la unión de los vértices centrales de cada cara del prisma.
Aquí observamos una dipirámide, es un poliedro formado por dos pirámides unidas, dual del prisma obtenido en la unión de los vértices centrales de cada cara del prisma. Vértices sobre caras: Otra posible inscripción de poliedros regulares: un tetraedro regular inscrito en un octaedro regular, tomando de este último los puntos medios de algunas caras (de todas tendríamos en este caso el cubo, su dual). Como los dos poliedros no son duales no cogemos todos los puntos de cada cara sino sólo algunos.
Vértices sobre caras: Otra posible inscripción de poliedros regulares: un tetraedro regular inscrito en un octaedro regular, tomando de este último los puntos medios de algunas caras (de todas tendríamos en este caso el cubo, su dual). Como los dos poliedros no son duales no cogemos todos los puntos de cada cara sino sólo algunos.